Challenges¶
Challenge 1: Explore how to define desired states¶
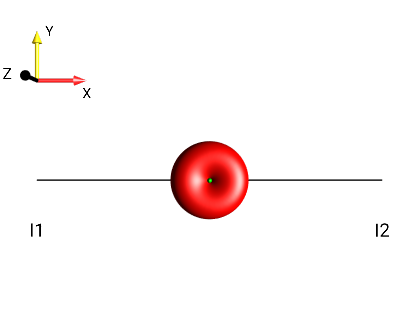
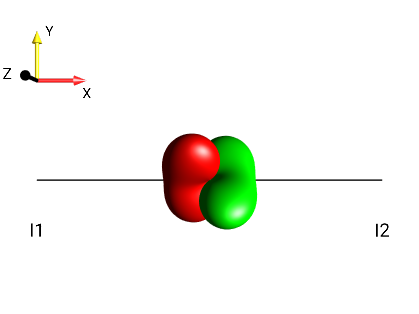
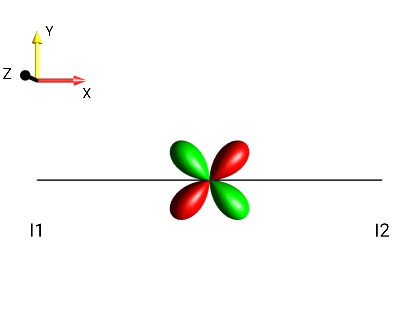
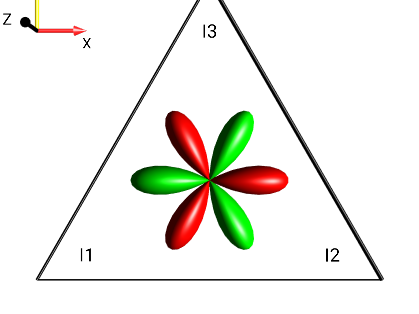
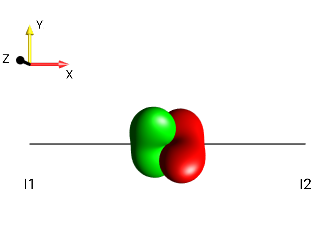
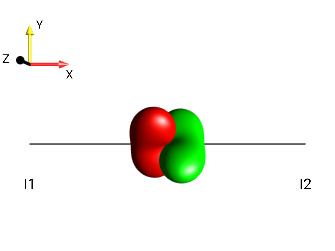
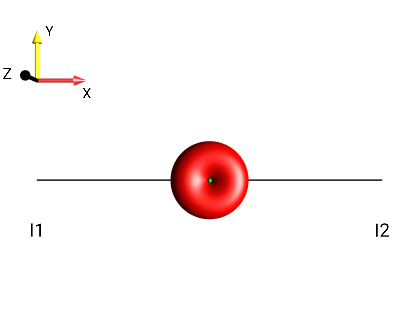
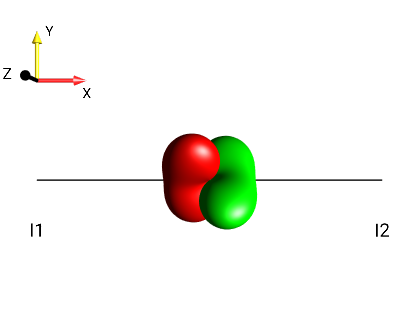
Create the following droplets using the menu :
|
|
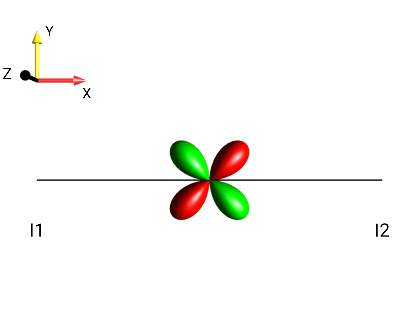
|
|
?
?
?
?
Challenge 2: Explore how to define desired states¶
Create the following droplets using the menu :
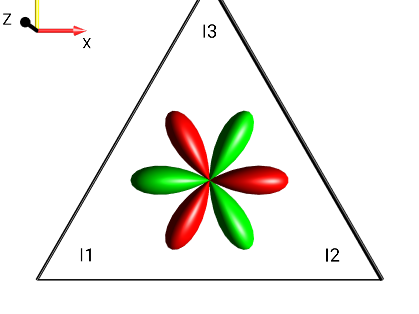
|
|
|
?
?
?
Solution 2¶
(turn off the preference Magnetization Vectors to get an opaque droplet).
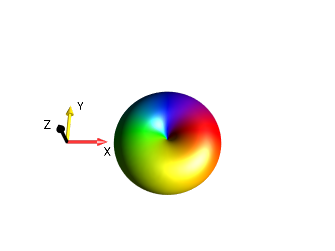
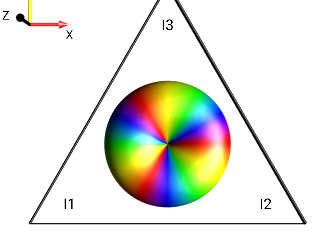
Fig. 218 \(I_{1}^{-}\)¶
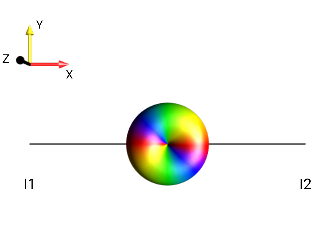
Fig. 219 \(I_{1}^{+}I_{2}^{+}\)¶
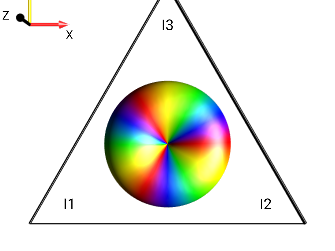
Fig. 220 \(2 \cdot I_{1}^{-}I_{2}^{-}I_{3}^{-}\)¶
Challenge 3: Explore how to define desired states¶
Create the following droplets using the menu :
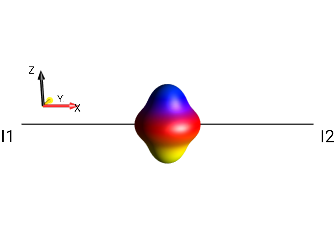
|
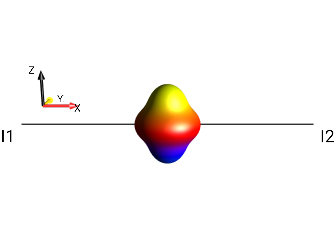
|
|
?
?
?
Challenge 4: Explore how to interpret droplets¶
Using the menu , create the operator 2Qx(I1,I2) and determine how it can be expressed as a linear combination of Cartesian product operators.
Solution 4¶
The double-quantum x operator involving spins I1 and I2 corresponds to the following droplet:
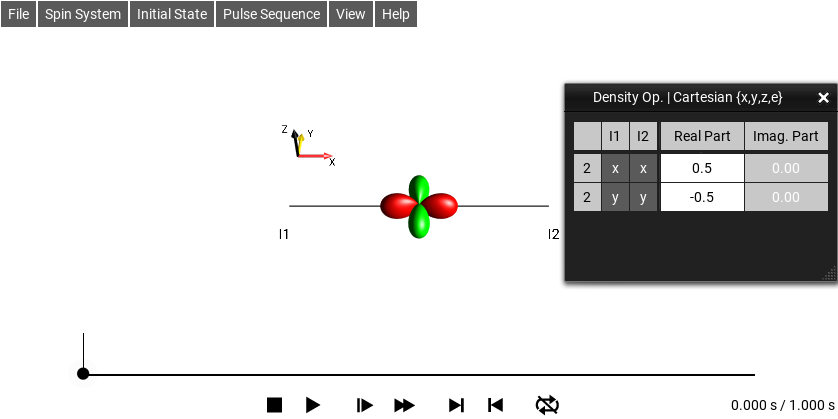
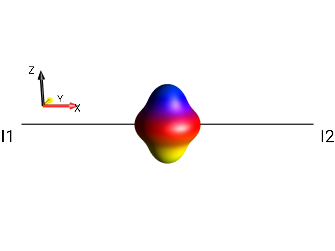
Fig. 224 \(\rho_0 = I_{1x}I_{2x}-I_{1y}I_{2y}\)¶
Select the menu to see the operator decomposition. The Cartesian terms will be displayed in the shorthand notation for Cartesian operators as shown in Fig. 224.
Hence, \(2Qx(I1,I2) = 0.5 (2I_{1x}I_{2x}) - 0.5 (2I_{1y}I_{2y}) = I_{1x}I_{2x} - I_{1y}I_{2y}\).
Challenge 5: Explore how to interpret droplets¶
Using the menu , create the operator \(2I_{1}^{+}I_{2}^{+}I_{3}^{+}\) and determine how it can be expressed as a linear combination of Cartesian product operators.
Solution 5¶
The +3-quantum operator \(2 \cdot I_{1}^{+}I_{2}^{+}I_{3}^{+}\) corresponds to the following droplet:
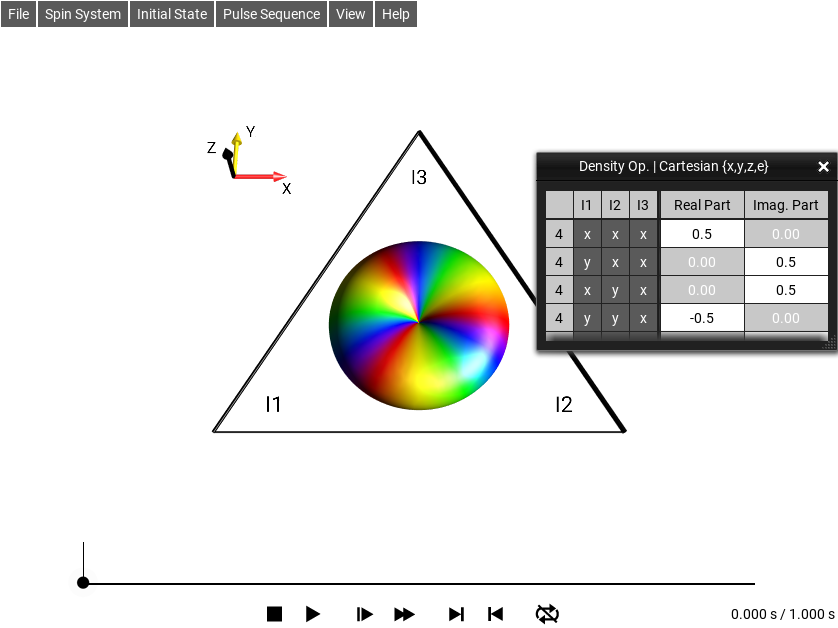
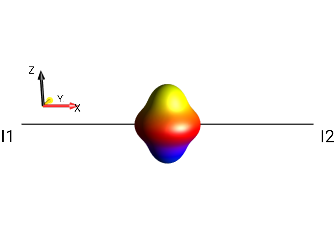
Fig. 225 \(\rho_0 = 2 \cdot I_{1}^{+}I_{2}^{+}I_{3}^{+}\)¶
Select the menu . The following terms will be displayed in the shorthand notation for Cartesian operators as shown in Fig. 225.
Hence,
Challenge 6: Pulse sequence design challenge¶
Suppose in the course of a pulse sequence, you have created the state \(I_{1z}I_{2z} - I_{1y}I_{2y}\). How can you transfer this state into ±2 quantum coherence by a single pulse?
Solution 6¶
Using the menu , create the operator \(I_{1z}I_{2z} - I_{1y}I_{2y}\). The corresponding DROPS representation should look like:
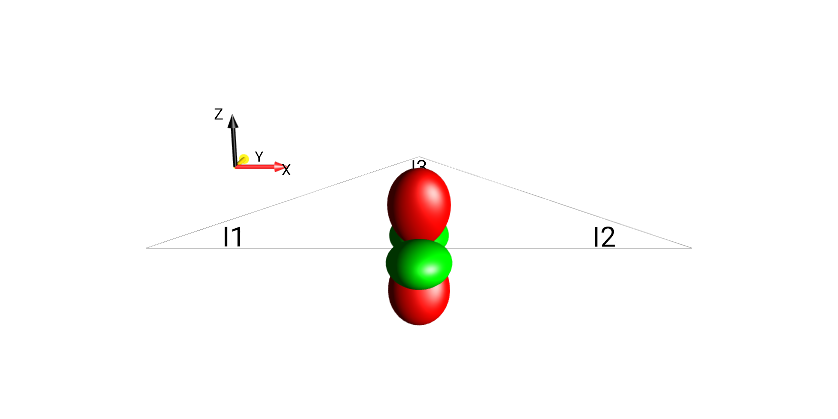
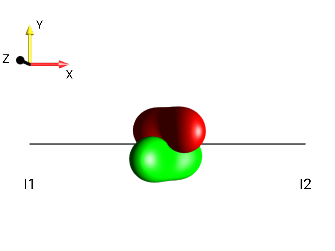
Fig. 226 \(I_{1z}I_{2z}-I_{1y}I_{2y}\)¶
The droplet representing the bilinear terms involving spins I1 and I2 already has the desired shape and color of ±2 quantum coherence, except that it is not correctly oriented! Rotating it by 90° around the y (or −y) axis will yield the correct orientation, i.e. a non-selective 90°y (or a 90°−y) pulse yields the desired ±2 quantum coherence. This can be tested by selecting and the resulting DROPS representation at the end of the pulse is shown on the right. (Note the rectangle at the bottom, which represents the pulse, where the blue color represents the pulse phase −y.)
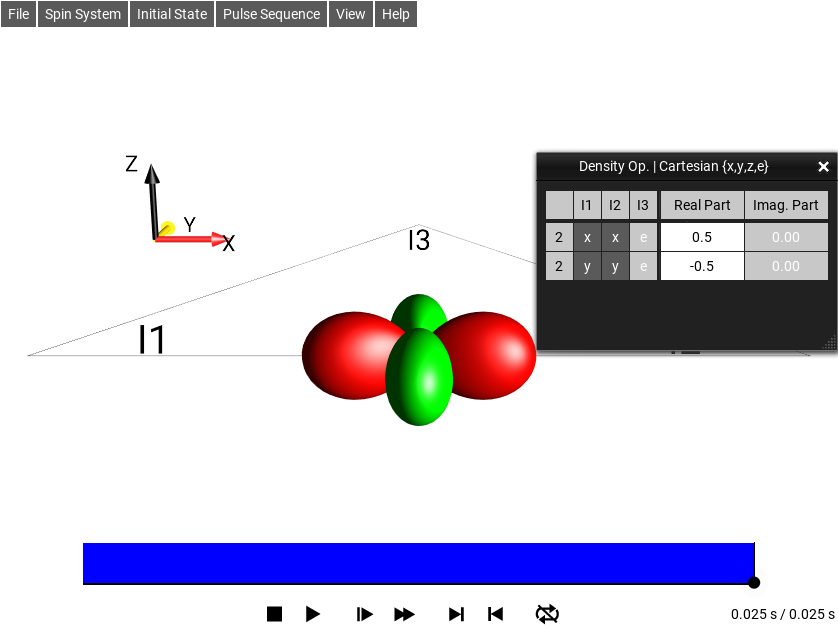
Fig. 227 \(\rho_0 = I_{1z}I_{2z}-I_{1y}I_{2y}\)¶
Challenge 7: Define a new operator¶
Display the droplet corresponding to the operator \(2I_{1x}I_{2x} + i 2I_{1z}I_{2x}\). (When the droplet is oriented properly, you will see the SpinDrops logo.)
Solution 7¶
Using the menu ,
create the operator \(2I_{1x}I_{2x} + i 2I_{1z}I_{2x}\). Orienting the
resulting droplet in the Drops display such that the view direction is
along the y axis yields the SpinDrops logo :-)
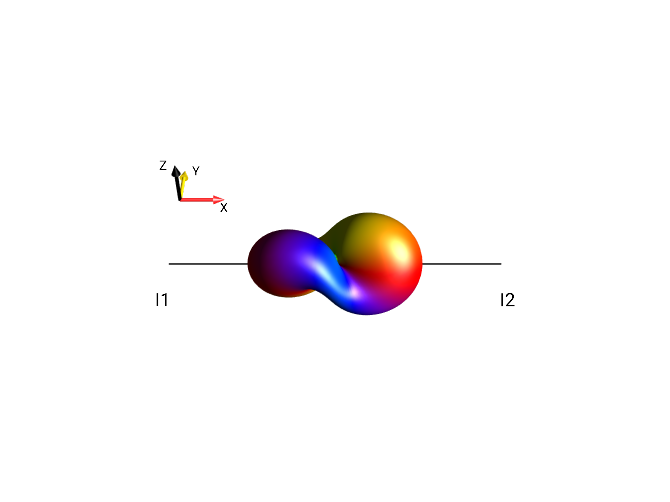
Challenge 8: Rotations of operators and droplets¶
Starting from the term \(2I_{1x}I_{2y}\), find a sequence of non-selective rotations (90±x, 90±y, or 90±z) to incrementally create all of the bilinear operators of the form \(2I1_aI2_b\) with \(a≠b\) and \(a,b ∈ {x,y,z}\).
Solution 8¶
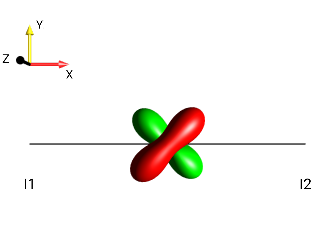
|
\(90°_x \rightarrow\) |
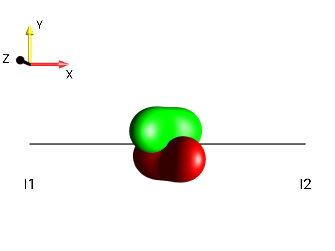
|
\(90°_z \rightarrow\) |
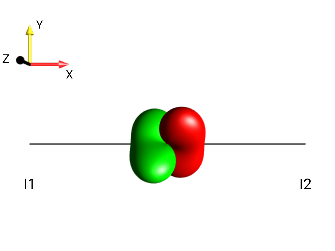
|
\(90°_y \uparrow\) |
\(90°_y \downarrow\) |
|||
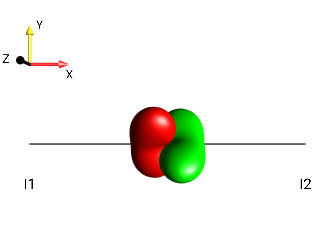
|
\(\leftarrow 90°_x\) |
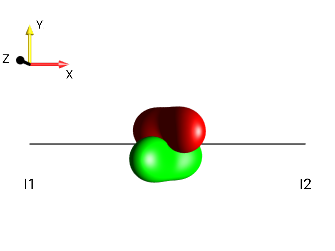
|
\(\leftarrow 90°_x\) |
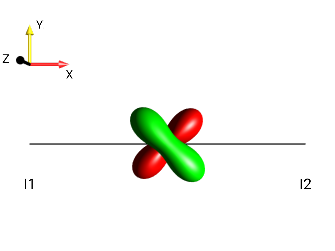
|
Challenge 9: Recognizing droplets of antiphase operators (A)¶
Determine for each of the following droplets whether it represents antiphase coherence with respect to the first spin (\(±2I_{1z}I_{2a}\) with \(a ∈ \{x,y\}\) ) or with respect to the second spin (\(±2I_{1a}I_{2z}\) with \(a ∈ \{x,y\}\) )!

|

|
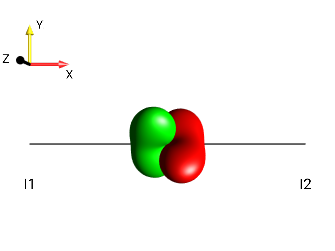
|

|

|
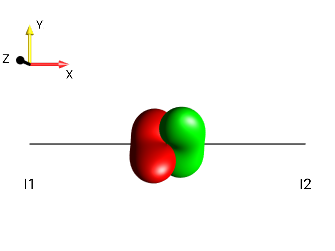
|
Solution 9¶
This challenge can be solved by simply observing the “kissing beans’ head tilt” (c.f. Head-tilt Rule).
right tilt 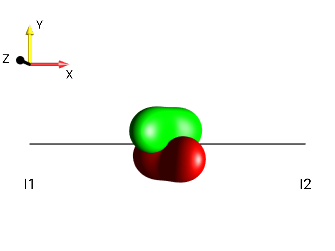
Fig. 228 \(±2I_{1a}I_{2z}\)¶ |
left tilt 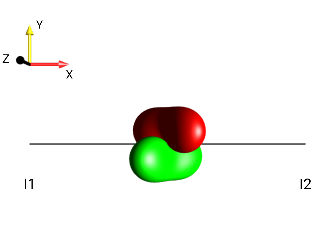
Fig. 229 \(±2I_{1z}I_{2a}\)¶ |
left tilt 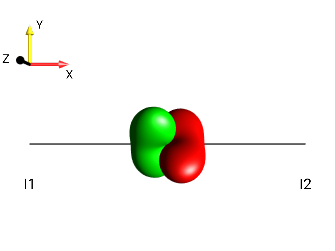
Fig. 230 \(±2I_{1z}I_{2a}\)¶ |
right tilt 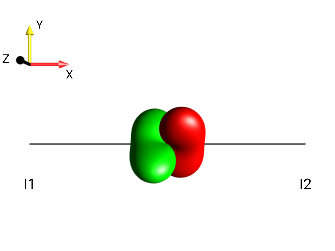
Fig. 231 \(±2I_{1a}I_{2z}\)¶ |
left tilt 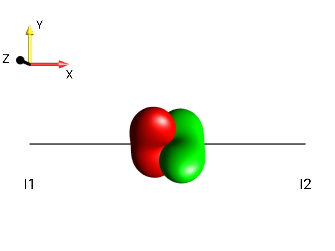
Fig. 232 \(±2I_{1z}I_{2a}\)¶ |
right tilt 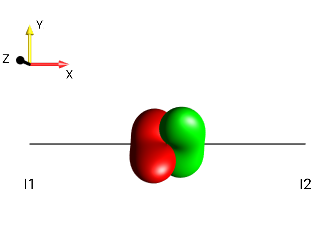
Fig. 233 \(±2I_{1a}I_{2z}\)¶ |
Challenge 10: Recognizing droplets of antiphase operators (B)¶
Determine for each of the droplets the exact form of the corresponding antiphase operator!

|

|

|

|

|

|
Challenge 11: Symmetry of antiphase operators under 180° rotations (A)¶
Verify that the following symmetry relations of anti-phase operators under 180° rotations are faithfully represented by the corresponding antiphase droplets!
\(2I_{1x}I_{2z} \xrightarrow{180°x} -2I_{1x}I_{2z}\) |
\(2I_{1x}I_{2z} \xrightarrow{180°y} 2I_{1x}I_{2z}\) |
\(2I_{1x}I_{2z} \xrightarrow{180°z} -2I_{1x}I_{2z}\) |
\(2I_{1y}I_{2z} \xrightarrow{180°x} 2I_{1y}I_{2z}\) |
\(2I_{1y}I_{2z} \xrightarrow{180°y} -2I_{1y}I_{2z}\) |
\(2I_{1y}I_{2z} \xrightarrow{180°z} -2I_{1y}I_{2z}\) |
Solution 11¶
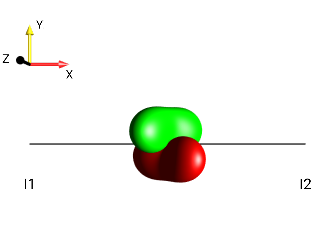
Fig. 240 \(2I_{1x}I_{2z}\)¶ |
\(180°_x \rightarrow\) |
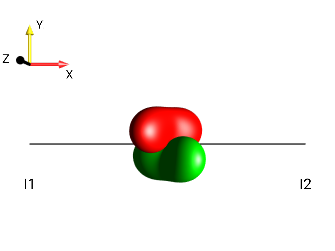
Fig. 241 \(-2I_{1x}I_{2z}\)¶ |

Fig. 242 \(2I_{1x}I_{2z}\)¶ |
\(180°_y \rightarrow\) |

Fig. 243 \(2I_{1x}I_{2z}\)¶ |

Fig. 244 \(2I_{1x}I_{2z}\)¶ |
\(180°_z \rightarrow\) |

Fig. 245 \(-2I_{1x}I_{2z}\)¶ |
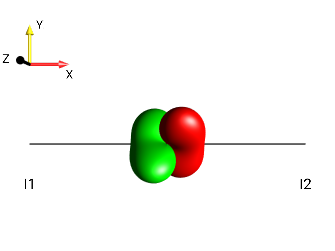
Fig. 246 \(2I_{1y}I_{2z}\)¶ |
\(180°_x \rightarrow\) |

Fig. 247 \(2I_{1y}I_{2z}\)¶ |

Fig. 248 \(2I_{1y}I_{2z}\)¶ |
\(180°_y \rightarrow\) |
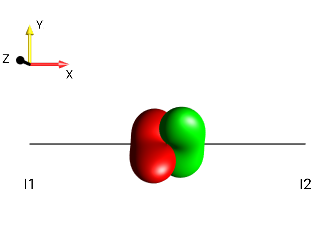
Fig. 249 \(-2I_{1y}I_{2z}\)¶ |

Fig. 250 \(2I_{1y}I_{2z}\)¶ |
\(180°_z \rightarrow\) |

Fig. 251 \(-2I_{1y}I_{2z}\)¶ |
Challenge 12: Comparing the speed of coherence transfer¶
Compare the time required to transfer the initial state \(I_{1x}\) to \(I_{2x}\) in a homonuclear two-spin system when using either a sequence of delays and pulses (such as in a fully refocused INEPT) or an isotropic mixing sequence (TOCSY) for a given coupling constant J12. Which sequence is faster and by how much?
Solution 12¶
For J12 = 1 Hz (and v1 = v2 = 0 Hz), simulations are shown for the sequence 1/(2J12) - 90°x - 1/(2J12) (Fig. 252) and for isotropic mixing (Fig. 253). The isotropic mixing sequence only requires half the amount of time compared to the INEPT-type transfer, i.e. it is twice as fast. The times shown in these examples are not related exactly by a factor of two (1.025 s and 0.5 s) because the 1.025 s includes the 0.025 second 90°x pulse duration, from a pulse amplitude of 10 Hz, but in a real experiment would be extremely short due to much higher actual pulse amplitudes (typically on the order of 1 kHz - 20 kHz).
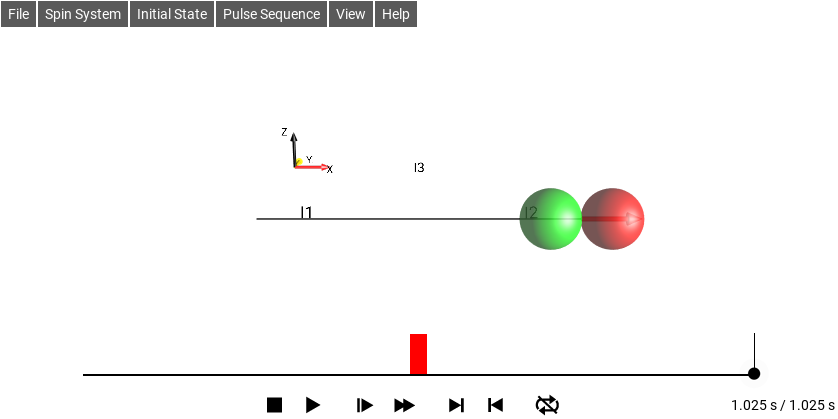
Fig. 252 On-resonance Magnetization Transfer Sequence¶
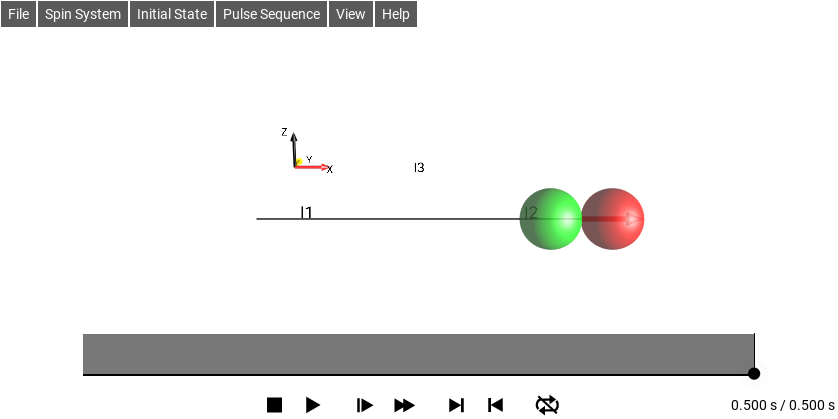
Fig. 253 Isotropic Mixing Sequence¶
Challenge 13: Seeing coherence orders¶
Which coherence orders \(p\) are contained in the following operators?
a 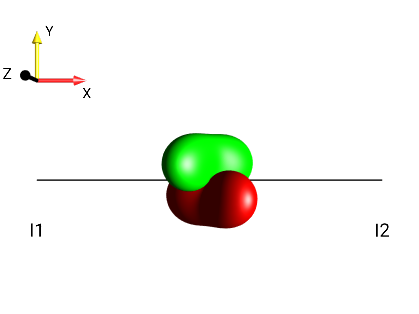
Fig. 254 \(2I_{1x}I_{2z}\)¶ |
b 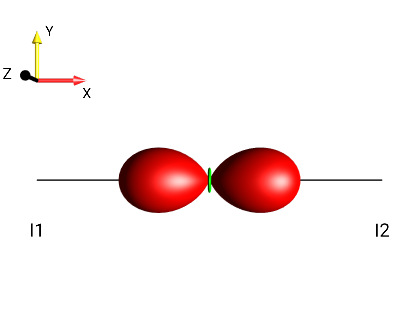
Fig. 255 \(2I_{1x}I_{2x}\)¶ |
c 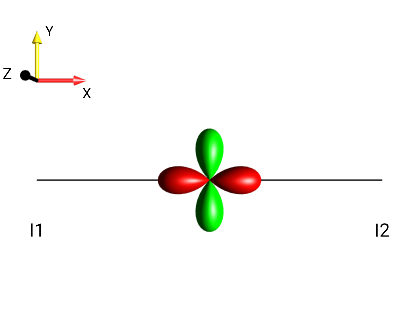
Fig. 256 \(I_{1x}I_{2x}-I_{1y}I_{2y}\)¶ |
d 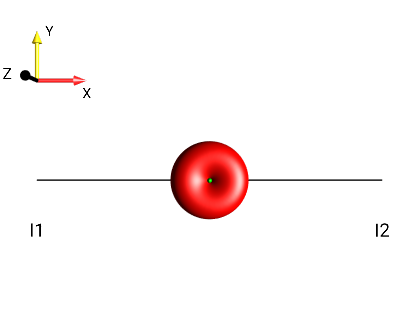
Fig. 257 \(I_{1x}I_{2x}+I_{1y}I_{2y}\)¶ |
Solution 13¶
Create the terms using the menu. Choose to see the corresponding droplet terms separated based on coherence order:
a |
b |
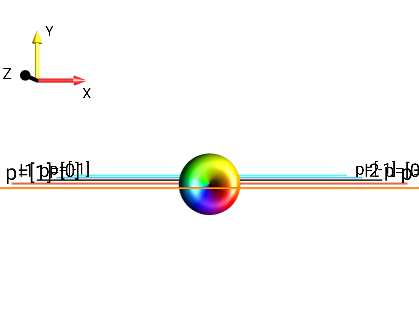
Fig. 258 \(2I_{1x}I_{2z}\)¶ |
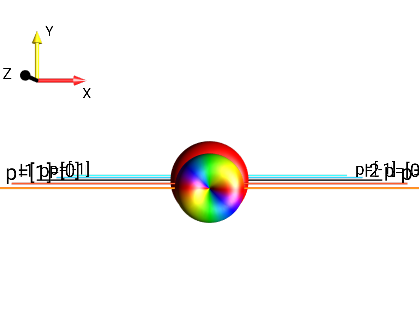
Fig. 259 \(2I_{1x}I_{2x}\)¶ |
\(p = +1,-1\) |
\(p = +2,0,-2\) |
c |
d |
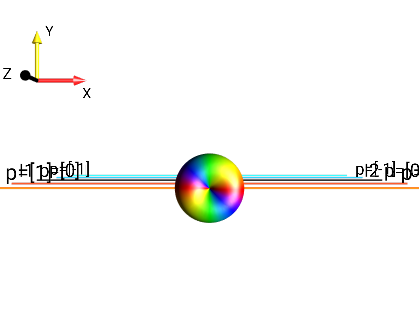
Fig. 260 \(I_{1x}I_{2x}-I_{1y}I_{2y}\)¶ |
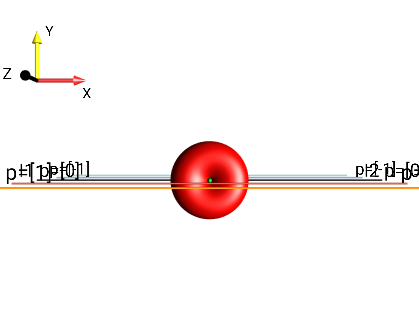
Fig. 261 \(I_{1x}I_{2x}+I_{1y}I_{2y}\)¶ |
\(p = +2,-2\) |
\(p = 0\) |