Mathematical Background¶
Mathematical Background of the DROPS Visualization¶
It is not necessary to understand the mathematical details of the mapping between quantum-mechanical operators and their DROPS representation in order to use the DROPS representation to visualize e.g. the state of a coupled spin system. Similar to how it is not necessary to understand the mathematical details of the mapping between quantum-mechanical operators for two-level systems and their vector representation via the expectation values of the spin operators \(I_x\), \(I_y\), and \(I_z\) in order to use the well-known vector picture to visualize the state of uncoupled spins.
Nonetheless, it may be interesting to learn more about the mathematical background of this mapping and the connection to Wigner representations. In the following, we summarize some of the underlying ideas. For details beyond this summary, we refer to the manuscript Visualizing states and operators of coupled spins systems [GARON2015] and to A. Garon’s thesis On a new visualization tool for quantum systems and on a time-optimal control problem for quantum gates [GARON2014], and related Mathematica package [GARONG2014].
Wigner Functions of Single Spins¶
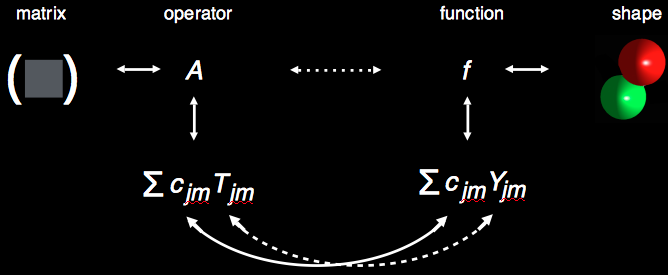
For a system consisting of just a single spin, it is always possible to express a related operator as a linear combination of tensor operators \(T_{jm}\) with (in general complex) coefficients \(c_{jm}\). This is also true for spins other than 1/2, and includes, for example, the density operator encoding the state of the spin.
By using the natural mapping between spherical tensor operators \(T_{jm}\) and spherical harmonics \(Y_{jm}\), is it possible to represent any operator \(A\) by a function \(f\) on a sphere, which can have complex values and which can be plotted as a three-dimensional shape: for a given point \(s\) of the unit sphere, the complex number \(f(s)\) can be written as \(r(s) e^{iφ(s)}\) which can be represented by a point with distance \(r(s)\) from the origin and a color to represent the phase \(φ(s)\) (see Color Code). If the operator \(A\) is a density operator, the function \(f\) is called a Wigner function.
DROPS Display and Wigner Representation of Coupled Spins¶
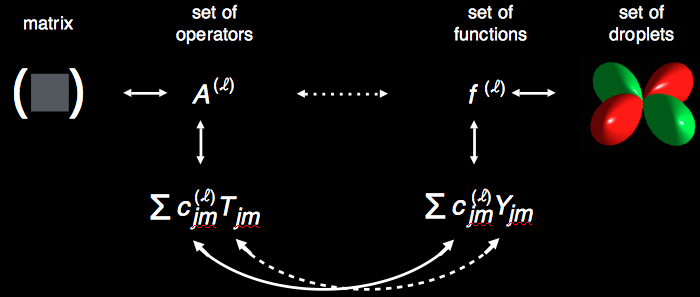
For systems of coupled spins, an operator \(A\) can be expressed as a linear combination of tensor operators. However, this basis contains multiple tensor operators with the same rank \(j\), which precludes a one-to-one map to the spherical harmonics \(Y_{jm}\). The problem can be alleviated by grouping the basis’ tensor operators into discrete sets (labeled \(l\)), where tensor operators with rank \(j\) appear not more than once in each set \(l\). As the tensor operators form a complete basis, any operator \(A\) can then also be decomposed into components that correspond to these discrete sets \(l\) of tensor operators:
Thus, analogously to the case of single spins, each component \(A^{(l)}\) can be mapped to a function \(f^{(l)}\) on a sphere and represented by a corresponding colored shape labeled \(l\).
This is the basic idea of the DROPS (Discrete Representation of spin OPeratorS) representation of operators. The individual shapes, \(l\), are called droplets. If the operator \(A\) is the density operator, the corresponding set of functions \(f^{(l)}\) forms a generalized Wigner representation.
Mapping of Operator Components \(A^{(l)}\) to Individual Droplets¶
If an operator \(A\) is decomposed as described above in the form \(A = \sum_l A^{(l)}\) then each of the operator components \(A^{(l)}\) can be represented by a function \(f^{(l)}\) on a sphere by mapping tensor operators \(T_{jm}\) to spherical harmonics \(Y_{jm}\) as in the case of single spins:
(non-)Hermitian Tensor Operators and Real vs. Complex Spherical Harmonics¶
The tensor operators \(T_{jm}\) have two forms: Hermitian and non-Hermitian. The [GARON2015] paper uses the non-Hermitian form. A transformation is applied to these non-Hermitian tensor operators \(T_{jm}\) as well as the complex spherical harmonics \(Y_{jm}\), resulting in Hermitian tensor operators and real spherical harmonics.
Using the real spherical harmonics greatly simplifies the calculation of the spherical harmonic shapes for SpinDrops’ display. But it also means that the tensor basis must be the Hermitian tensor basis, deviating from the tensor basis used in the DROPS paper [GARON2015].
LISA Basis¶
There is no unique assignment of tensor operators \(T_j\) into discrete sets \(l\) constrained by the condition that a tensor operators \(T_j\) with rank \(j\) appears not more than once in each set. Depending on the application, different approaches to the assignment may be preferable. For applications with distinguishable spins, the so-called LISA basis [GARON2015] has a number of very favorable properties and provides an intuitive DROPS visualization to represent NMR experiments graphically. It groups tensor operators based on Linearity, Subsystems and Auxiliary (LISA) criteria, such as permutation symmetry. Applying these criteria constrains a unique grouping, which defines the tensor operators of the basis up to their algebraic signs. In the standard LISA basis the signs are chosen to result in intuitive shapes [GARON2015]. The LISA basis is the default basis used by SpinDrops to draw the DROPS.
Plain-text entry of the LISA basis is described in detail in the section PTON for the LISA basis.
Tensor Grouping in the LISA basis¶
In the standard LISA basis, the following criteria are used for the grouping of tensor operators into discrete sets \(l\) such that each set contains not more than one tensor of the same rank \(j\).
Linearity¶
The first criterion for the grouping of tensors is the number \(k\) of involved spins, which is also called the linearity of an operator. For three-spin systems, the linearity \(k\) can be 0, 1, 2, or 3. Except for \(k=0\), the resulting groups still contain several tensors with the same rank \(j\).
Subsystems¶
The second criterion is based on the subset \(K\) of spins that are involved in a tensor operator. In a system consisting of three spins, the subsets are, for linear operators \((k=1)\): \(\{I1\}\), \(\{I2\}\), and \(\{I3\}\), for bilinear operators \((k=2)\): \(\{I1,I2\}\), \(\{I1,I3\}\), and \(\{I2,I3\}\). In linear and bilinear subsystems, not more than one tensor exists with the same rank \(j\), so these groups can be simply labeled according to their associated spins, however, this is not the case for the trilinear operators \((k=3)\), i.e. for trilinear tensors involving all spins \(\{I1, I2, I3\}\), thus the introduction of Auxiliary Criteria and unique \(τ\) grouping labels.
Auxiliary Criteria¶
For \(k>2\), auxiliary criteria are needed in order to define unique groupings of tensors. In the LISA basis, after subsystem, the next criterion for the grouping of tensors is based on permutation symmetry. For systems of up to five spins, this is sufficient to define a unique and physically motivated grouping such that all tensors within each group have different ranks \(j\).
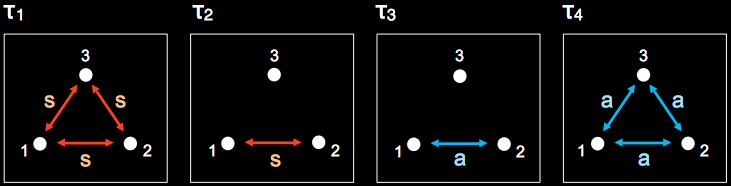
Tensor Groups for 3-spin system¶
The LISA grouping of tensors is schematically summarized below. For each linearity \(k\) and subsystem \(K\), the rank \(j\) of the existing tensor operators is indicated. For the trilinear terms \((k=3)\), also the permutation symmetry is indicated (in terms of so-called Young Tableaux, see [GARON2015], which is used as an auxiliary criterion to define sets of tensors in which all ranks \(j\) are different. The table also indicates the labels \(l\) of the resulting unique sets of tensor operators and of the corresponding droplets in the DROPS representation.
Linearity \(k\) |
Subsystem |
Rank \(j\) |
Permutation Symmetry (ranks) |
Set Label \(l\) |
|
0 |
\(\emptyset\) |
0 |
\(I_d\) |
|
|
1 |
\({I_1}\) \({I_2}\) \({I_3}\) |
1 1 1 |
\(I_1\) \(I_2\) \(I_3\) |
|
|
2 |
\({I_1,I_2}\) \({I_1,I_3}\) \({I_2,I_3}\) |
2,1,0 2,1,0 2,1,0 |
\(\{I_1,I_2\}\) \(\{I_1,I_3\}\) \(\{I_2,I_3\}\) |
|
|
3 |
\({I_1,I_2,I_3}\) |
3 2,2 1,1,1 0 |
\({\tau_1}\) (3,1) \({\tau_2}\) (2,1) \({\tau_3}\) (2,1) \({\tau_4}\) (0) |
\(\{\tau_1\}\) \(\{\tau_2\}\) \(\{\tau_3\}\) \(\{\tau_4\}\) |
|
Spin Permutations¶
The trilinear operators corresponding to the sets \(τ_1\), \(τ_2\), \(τ_3\), and \(τ_4\) have characteristic symmetries with respect to permutations of spin labels. As illustrated schematically below, the tensor operators in set \(τ_1\) are symmetric (s) with respect to any pairwise exchange of spin labels, i.e. any exchange of spin labels leaves these operators invariant. Conversely, the operators in set \(τ_4\) are anti-symmetric (a) with respect to any pairwise exchange of spin labels, i.e. any exchange of spin labels changes the sign of these operators. The tensor operators in set \(τ_2\) are symmetric (s) only with respect to the exchange of spin labels 1 and 2, whereas the tensor operators in set \(τ_3\) are anti-symmetric (a) with respect to the exchange of spin labels 1 and 2.
More Spin Permutations¶
The symmetry of the droplets \(τ_1\), \(τ_2\), \(τ_3\), and \(τ_4\) with respect to permutations of spin labels is illustrated for the operator \(4I_{1x}I_{2y}I_{3z}\) (a). Permuting spins 1 and 2 results in the operator (b) \(4I_{1y}I_{2x}I_{3z}\) and as expected, the droplets \(τ_1\) and \(τ_2\), which are symmetric under the (1,2) permutation, are unchanged. In contrast, the droplets \(τ_3\) and \(τ_4\), which are anti-symmetric with regard to this operation, change sign (resulting in inverted colors). The (1,3) permutation results in the operator \(4I_{3x}I_{2y}I_{1z}\) => \(4I_{1z}I_{2y}I_{3x}\) (c) and the (2,3) permutation results in the operator \(4I_{1x}I_{3y}I_{2z}\) => \(4I_{1x}I_{2z}I_{3y}\) (d). As discussed above, droplet \(τ_1\) is also symmetric with respect to these permutations and is identical to case (a). Droplet \(τ_4\) is anti-symmetric with respect to these permutations, resulting in a color change from red to green.
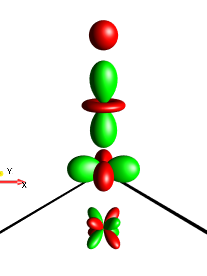
Fig. 155 \(4I_{1x}I_{2y}I_{3z}\)¶ |
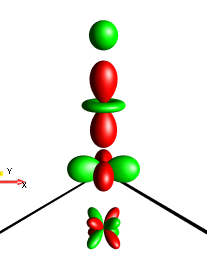
Fig. 156 \(4I_{1y}I_{2x}I_{3z}\)¶ |
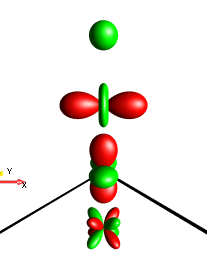
Fig. 157 \(4I_{1z}I_{2y}I_{3x}\)¶ |
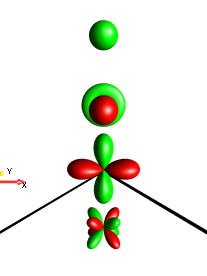
Fig. 158 \(4I_{1x}I_{2z}I_{3y}\)¶ |
Coherence Order¶
An operator \(A\) has a well-defined coherence order \(p\) if a rotation around the z axis by an arbitrary angle α reproduces the operator \(A\) up to an additional phase factor \(exp(-ipα)\), i.e. if
Similarly, a droplet representing a function \(f(l)\) corresponds to an operator term \(A(l)\) with well-defined coherence order \(p\), if a rotation around the z axis by an arbitrary angle \(α\) reproduces the droplet up to an additional phase factor \(exp(-ipα)\). For simplicity, in the following we drop the superscript “\((l)\)”. For example, let us consider the rotation of the following droplet with \(p=+1\) by \(π/2\) (i.e. 90°) around the z axis:
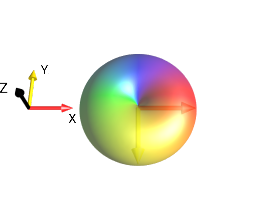
Fig. 159 \(\)¶ |
\(\xrightarrow[{\text{ around z Axis}}]{ \text{rotation by angle } \alpha=\frac{\pi}{2}}\) |
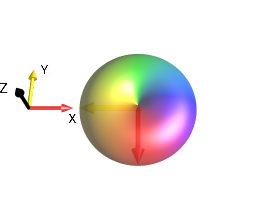
Fig. 160 \(\)¶ |
\(f(s)=r(s)e^{i\phi(s)}\) |
\(f'(s)=e^{ip\alpha}f(s) = r(s)e^{i\phi'(s)}\) with \(φ'(s) = φ(s) - pα = φ(s)-π/2\) |
For a droplet with coherence order \(p\), the corresponding function \(f(s) = r(s) e^{iφ(s)}\) is transformed by a z rotation with an angle α to \(f’(s) = r(s) e^{iφ’(s)}\) with \(φ’(s) = φ(s) - pα\).
To further illustrate this point, consider again \(p=+1\) and \(α=π/2\):
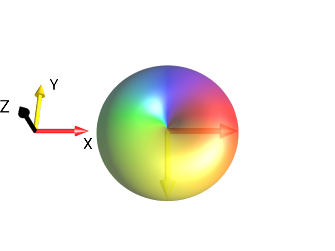
|
\[\xrightarrow[\text{ around z Axis}]{ \text{rotation by angle }
\alpha=\frac{\pi}{2}}\]
|
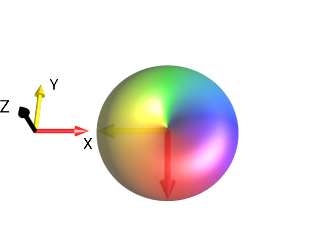
|
\(\uparrow\) |
\(\uparrow\) |
After the rotation, the shape of the droplet is the same but the color (representing the phase of the function \(f\)) has changed. Notice that the color of the point on the bottom of the drop (most negative in the y direction) has changed from yellow (corresponding to \(φ = π/2\)) to red (corresponding to \(φ’=0\)), which is expected from the general formula given above: