FAQ¶
What do I need to do to see the effect of a pulse sequence?¶
The simulation requires the definition of the spin system and its parameters (offset frequencies and coupling constants). Also make sure the desired initial state and the pulse sequence are specified. Then the simulation can be started with the play button and the DROPS display shows the effect on the state of the spin system in real time.
How can I see what a particular operator looks like?¶
Simply define the operator of interest in the menu
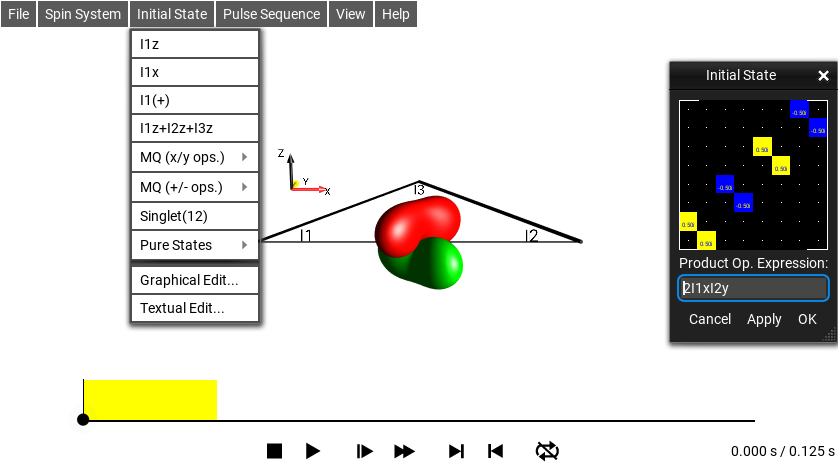
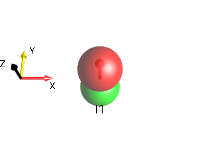
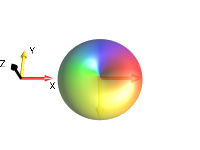
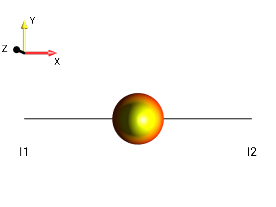
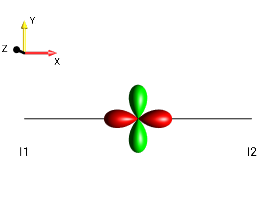
Fig. 262 \(\rho_0 = 2I_{1x}I_{2y}\)¶
In this example, the operator \(2I_{1x}I_{2y}\) is displayed.
(In the menu , it is
defined using the short-hand notation 2I1xI2y.)
Tip 1: Before defining the operator, make sure the time slider is at the beginning of the selected pulse sequence. (In order to actually see the defined operator and not what it has evolved to during the pulse sequence.) A simple way to do this is to press the
 button.
button.Tip 2: The triangle can be removed by setting all couplings to 0 Hz (open ). To hide the parameter sliders, just close the window.
How can I see which product operators are represented by a given DROPS display?¶
To see the current list of product operators, select
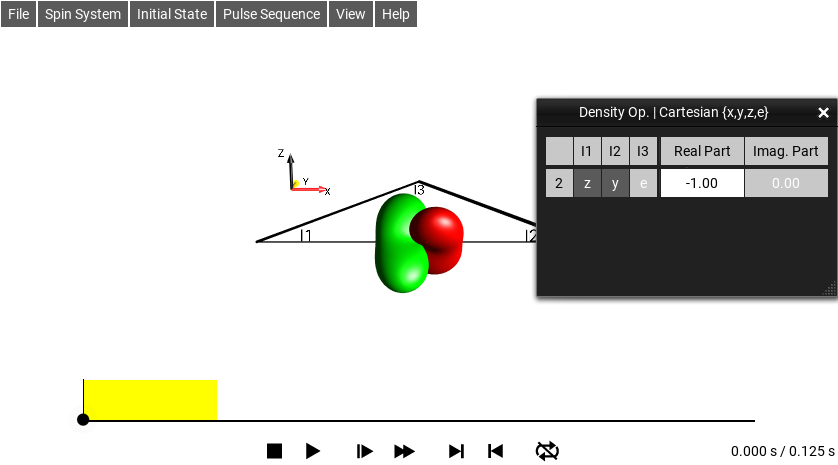
Fig. 263 Cartesian Product Operator List¶
The Cartesian product operator terms are displayed using the three-letter (see short-hand notation).
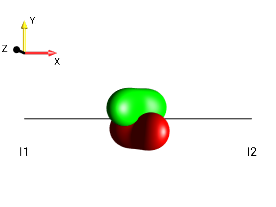
In this example, the DROPS display shows −1 zye, which is the
shorthand notation for the Cartesian product operator
\(-2I_{1z}I_{2y}\).
How can I see (and modify) the current frequency offsets and coupling constants of the spins system?¶
Select
The parameter sliders and the current values of the parameters are displayed in the System Parameters window.
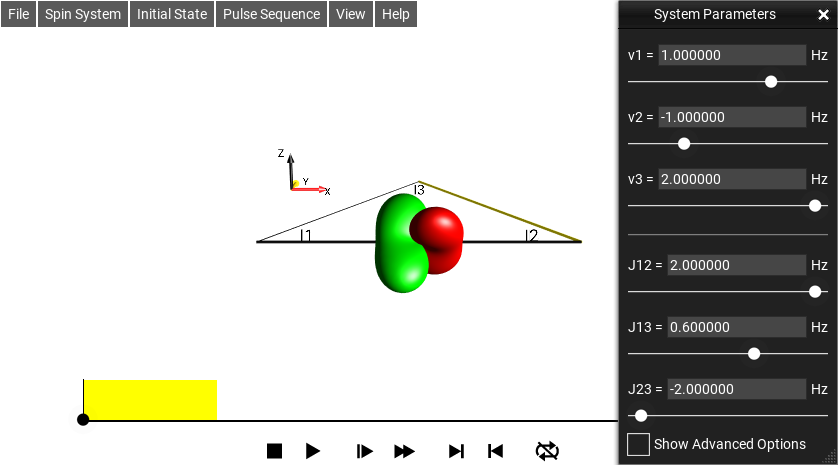
Fig. 264 Parameter Window¶
In this example, the offset frequencies of the first, the second, and the third spin are \(1 Hz\), \(-1 Hz\), and \(2 Hz\), respectively.
The coupling constants are \(J12 = 2 Hz\), \(J13 = 0.6 Hz\), and \(J23 = -2 Hz\).
Tip 1 The relative size and sign of the coupling constants is represented by the thickness and color (positive: white; negative: yellow) of the lines connecting the corresponding spins.
How do I choose the initial state of the spin system?¶
In the menu , a selection of initial states of interest is presented. In a typical experiments, you may be interested to start e.g. with z magnetization of the first spin of of all spins. Examples of operator you can select are given below:
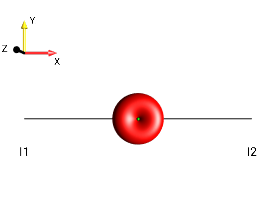
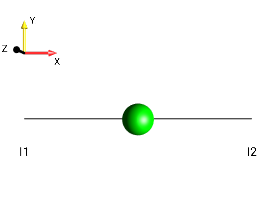
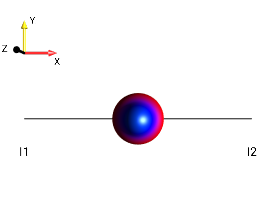
z magnetization of the first spin
x magnetization of the first spin
+1-quantum coherence of the first spin
z magnetization of the first, the second, and the third spin
Multiple-quantum operators with quantum order (+p) AND (-p) based real combination of Cartesian product operators
Multiple-quantum operators with quantum order (+p) OR (-p) based on raising and lowering operators
The traceless part of the singlet state involving the first and second spin
This option makes opens a window to edit the chosen initial density operator and generate any desired operator of interest
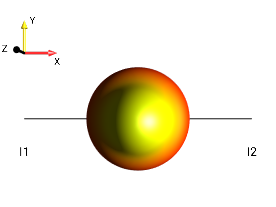
Examples of States and Droplets of a Single Spin¶
menu selection |
DROPS state |
|---|---|
|
|
|
|
|
|
|
|
|
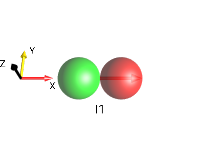
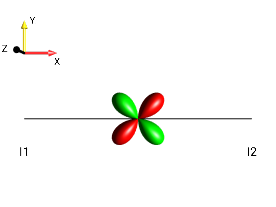
Examples of Zero-Quantum Coherences Involving Two Spins¶
menu selection |
DROPS state |
|---|---|
zero-quantum x coherence \(I_{1x}I_{2x} + I_{1y}I_{2y}\) |
|
zero-quantum y coherence \(I_{1y}I_{2x} - I_{1x}I_{2y}\) |
|
\(I_{1}^{+}I_{2}^{-}\) |
|
\(I_{1}^{-}I_{2}^{+}\) |
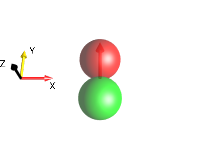
Examples of Single-Quantum Coherences Involving Two Spins¶
menu selection |
DROPS state |
|---|---|
antiphase x coherence \(2I_{1x}I_{2z}\) |
|
antiphase y coherence \(2I_{1y}I_{2z}\) |
|
+1 quantum antiphase coherence \(2I_{1}^{+}I_{2z}\) |
|
−1 quantum antiphase coherence |
Examples of Double-Quantum Coherences Involving Two Spins¶
menu selection |
DROPS state |
|---|---|
double-quantum x coherence \(I_{1x}I_{2x} − I_{1y}I_{2y}\) |
|
double-quantum y coherence \(I_{1y}I_{2x} + I_{1x}I_{2y}\) |
|
(+2)-quantum coherence \(I_{1}^{+}I_{2}^{+}\) |
|
(−2)-quantum coherence \(I_{1}^{-}I_{2}^{-}\) |
Additional Examples of Bilinear Operators Involving Two Spins¶
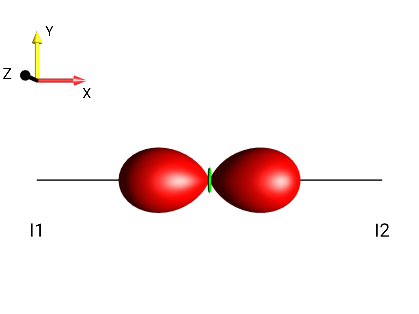
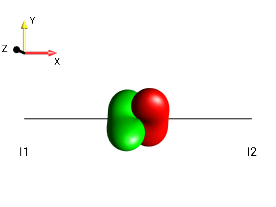
Fig. 265 \(2I_{1x}I_{2x}\)¶ |
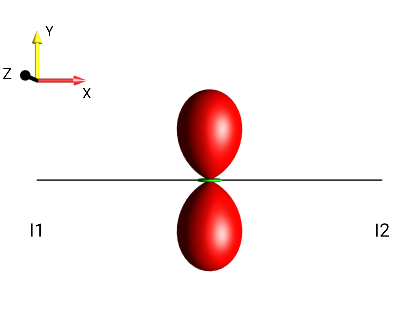
Fig. 266 \(2I_{1y}I_{2y}\)¶ |
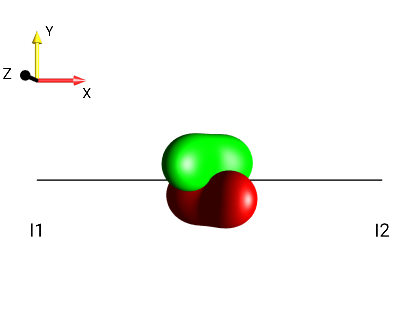
Fig. 267 \(2I_{1x}I_{2z}\)¶ |
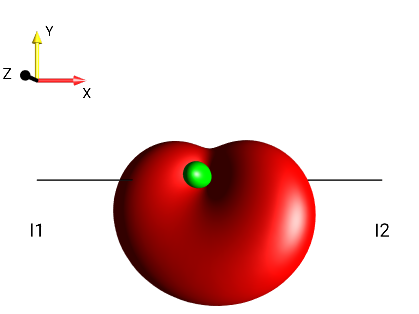
Fig. 268 \(2I_{1x}I_{2x}+2I_{1y}I_{2y}+2I_{1x}I_{2z}\)¶ |
How Can I Take a Screenshot of my DROPS Display on iOS?¶
A screen shot of the iPad or iPhone can be made by simultaneous clicking the home and power buttons.

The screenshot will be saved in the Camera Roll. To see the screen shot, use the standard “Photos” app on the home screen.